*Geek Box: Cohen’s d Measure of Effect Size
The Cohen’s d is a measure of effect size, most commonly used in behavioural science, for example psychology. It compares two means: one from a treatment group and one from a control group or comparison group.
The difference between the Cohen’s d and a p-values is that the p-value simply tells you whether there is an effect that is statistically significant, while the Cohen’s d tells you the size of the effect, i.e., how much did the magnitude of effect in the treatment group differ to the magnitude of effect in the control group. Similar to the p-value being set at <0.05 for significant being arbitrary, interpreting the Cohen’s d results have been subject to similar classifications, with an 0.2, 0.5, and 0.8 considered small, medium, and large, respectively. What these numbers represent is units of standard deviation. The Cohen’s d is based on the mean level in an overall distribution of data . Therefore the Cohen’s d value represents the standard deviation of the treatment group from the mean.
Look at the figure below: you can see the dark and light blue respective distributions overlap [shaded in green]. You can see the mean of the control group is the dotted horizontal white line in the dark blue distribution. And you can see the treatment group mean effect is the corresponding dotted horizontal white line in the light blue distribution: this is 1.6 standard deviations from the mean of the control group. The green shading is also important: it represents that there are still many individuals who do not fall within either distribution.
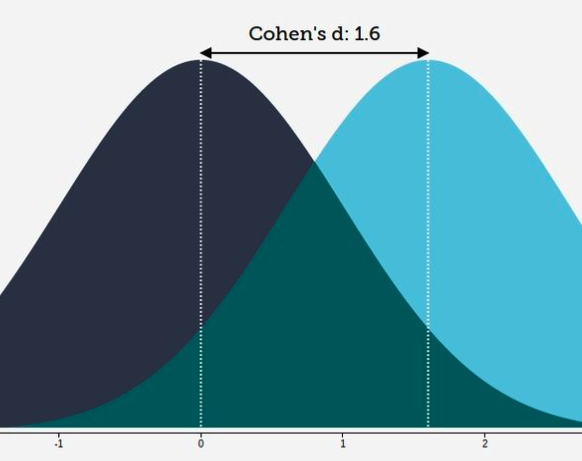
The effect size interpretation for Cohen’s d is just a general guideline and – similar to the way in which a statistically insignificant finding does not mean ‘there is no effect’ – the relevance of a ‘small’ or ‘large’ effect size will depend on the exposure and specific context being studies. A Cohen’s d of 0.4, for example, may be small-medium, but represents a clinically meaningful difference.
