*Geek Box: Assumptions of Mendelian Randomisation
All MR studies start with a genetic variant, which for an MR is known as an “instrumental variable”, or IV. The best way to illustrate these concepts is with the use of ‘directed acyclic graphs’, or DAG. DAG are graphs which illustrate the direction of relationships and are useful to illustrate causal concepts. Here is a DAG for MR:
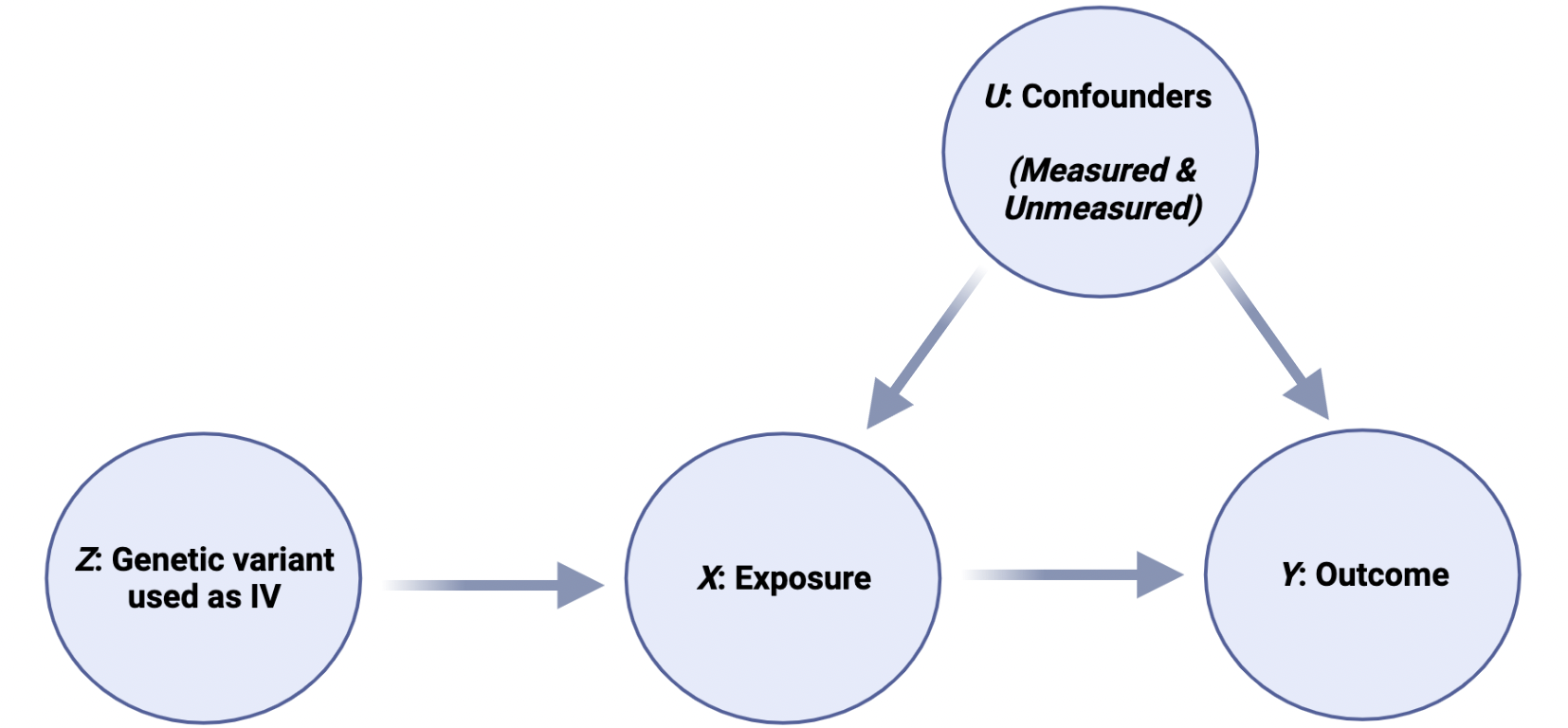
In this illustration, Z is the IV, a genetic variant associated with X, where X is the risk factor or “exposure”. For example, Z could be a genetic variant which results in more LDL-receptors, which means that X would be low blood LDL-C levels. Y is the outcome, in this example, CVD. Thus, this graph is depicting the causal effect of X [low LDL-C] on Y [CVD]. Finally, U is any unmeasured confounder, i.e., “residual confounding”. So, an MR study uses an IV [Z] to act as a proxy for an intervention of X on outcome Y.
For an IV [Z in our graph above] to be valid, it must meet three assumptions:
- Relevance: The genetic variant, Z, is robustly associated with the risk factor, X
- Exchangeability: The genetic variant is independent of confounders, U
- Exclusion-restriction: The genetic variant has no effect on the outcome, Y, i.e., Z only influences Y through the exposure, X.
An IV is only valid where the 3 assumptions above hold. This is crucial, because it means that claims of “causality” can only be made where these assumptions are met. However, in practice there is no easy way of testing that all assumptions hold, unlike in other statistical methods where the assumptions can be tested [e.g., the assumption that data follows a normal distributed can be tested with both statistical tests and by visual inspecting normality graphs].
In reality, the assumptions are addressed by considering different factors, e.g., the biological plausibility of the IV [i.e., is it biologically plausible that a gene that effects the LDL-receptor would lower LDL-C levels], by examining whether the estimates of the effect of the risk factor X on the outcome Y are similar across different analyses [i.e., does low LDL-C from different LDL-receptor variants have similar effects on CVD], and by considering whether the effects are not modified by other factors.
